未来边缘
0%

基于 BIP-32 和 BIP-39 规范生成 HD 钱包（分层确定性钱包）

Posted on Edited on In ,

关于 Bitcoin 的钱包

在 Bitcoin 中有两种主要类型的钱包，分别为：

  1. 非确定性钱包（Nodeterministic Wallet）：该钱包中的每个密钥都是从不同的随机数独立生成的，密钥彼此之间没有任何关系，这种钱包也被称为 JBOK 钱包（Just a Bunch Of Keys）；
  2. 确定性钱包（Deterministic Wallet）：其中所有的密钥都是从一个主密钥派生出来的，这个主密钥就是种子（seed），在该类型的钱包中，所有的密钥之间都是相互关联的，如果有原始种子，就可以再次生成全部的密钥；在确定性钱包中，可以使用不同的密钥推导方式。目前最常用的推导方法是 树状结构，也称为 分层确定性钱包 或 HD 钱包；

我们文章的目的就是生成 HD 钱包，HD 钱包 可以允许用户在不安全的服务器上使用，或者在每笔交易中使用不同的公钥。

涉及到钱包的一些常用标准规范有：

  • BIP-39: 助记词
  • **BIP-32**：HD 钱包
  • **BIP-43**：多用途 HD 钱包结构
  • **BIP-44**：多币种和多账户钱包

要生成钱包私钥，我们需要有个种子(seed)，而我们这里是通过助记词来生成的，下面我们就先了解一下如何基于 BIP-39 规范来生成助记词和种子(seed)。

关于 BIP-39

BIP-39 规范主要描述了基于助记词（一组便于记忆的单词）来生成确定性钱包的算法和过程。

该规范中主要由两部分构成：

  1. 如何生成助记词；
  2. 如何将生成的助记词转化成一个二进制种子；

下面就先分别介绍这两个部分来看看如何生成确定性钱包。

后面涉及到一些示例代码都是采用的 python-mnemonic 库。

生成助记词

生成助记词的算法过程如下图：

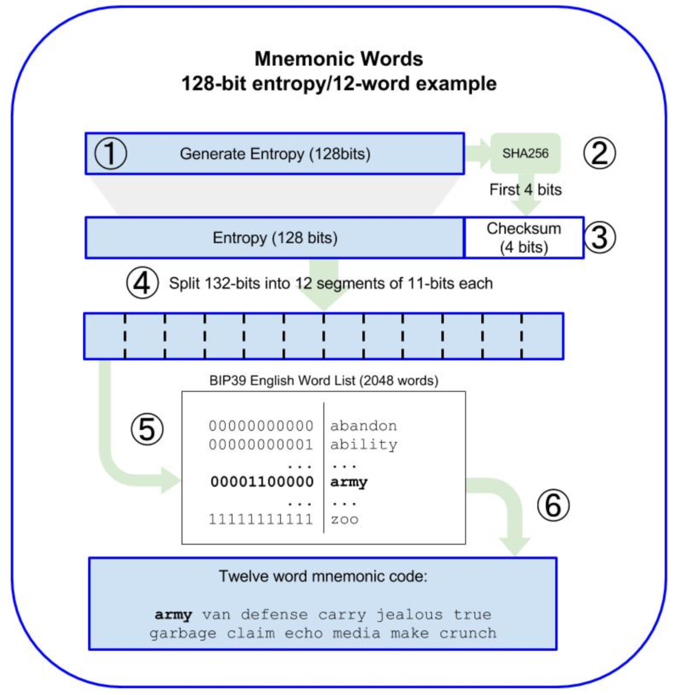
具体过程如下：

  1. 创建一个 128 到 256 位（步长 32 位）的随机序列（熵）；

    随机序列的长度称为 熵长，熵长按照步长 32 位，主要有几种分别为 [128, 160, 192, 224, 256]，我们示例图中是 128 位；

  2. 对上一步生成的随机序列进行 SHA256 生成 Hash 值，并取出该 Hash 值的前 N 位（熵长/32，如：128 位，则 N = 4）作为随机序列的校验和（Checksum）；
  3. 将 Checksum 添加至第一步生成的随机序列的尾部，此时对于图中示例加上 Checksum 之后为 128 + 4 = 132 位的随机序列；
  4. 将上一步的随机序列按照 11 位一段进行分隔(split)，这样对于 128 位熵长的序列就会生成 12 段（132/11=12）；
  5. 此时将每个包含 11 位部分的值与一个预定义的 2048 个单词的词典进行对应；
  6. 按照切割顺序生成了最终的单词组就是助记词；

可以看到不同熵长对应的 Checksum 的长度，最终生成的助记词的长度不同，具体如下表：

Entropy(bits) Checksum(bits) Entropy+Checksum(bits) Mnemonic length(words)
128 4 132 12
160 5 165 15
192 6 198 18
224 7 231 21
256 8 264 24

上面第 5 步涉及到单词表，理想的单词表应该满足智能选词、避免相似单词、排序单词表等特点，目前支持了多种不同国家的单词表。

如下示例代码基于 128 位强度的熵长生成了 12 个助记词：

1
2
3
4
5
6
>>> from mnemonic import Mnemonic
>>> m = Mnemonic('english')
>>> words = m.generate(strength=128)
>>> words
u'olympic hard body window sibling used only mimic put sad ability bone'
>>>

从助记词生成种子

助记词生成之后我们可以通过密钥生成函数 PBKDF2 算法来生成种子。

PBKDF2 需要提供两个参数：助记词和盐（salt）。其中 salt 的目的就是增加破解难度，而在 BIP-39 中，我们可以引入密码（passphrase）来作为保护种子的附加安全因素。

PBKDF2 is part of RSA Laboratories’ Public-Key Cryptography Standards (PKCS) series, specifically PKCS #5 v2.0, also published as Internet Engineering Task Force’s RFC 2898.

接着上面的助记词生成之后，如下图为生成 seed 的算法过程：

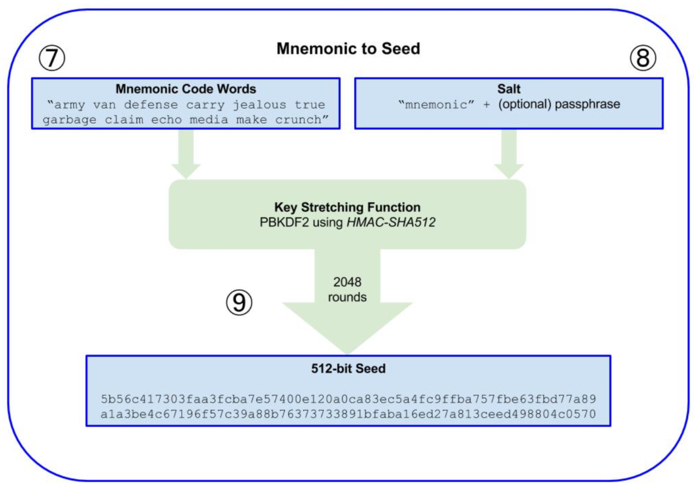
  1. PBKDF2 的第一个参数是上面生成的助记词；
  2. PBKDF2 的第二个参数就是 salt，一般有字符串和可选的用户提供的密码字符串连接组成；
  3. PBKDF2 使用 HMAC-SHA512 算法，使用了 2048 次 Hash 之后产生一个 512 位的值作为种子；

如下示例代码为基于上面示例中生成的助记词来生成种子：

1
2
3
4
5
6
7
8
>>> seed = Mnemonic.to_seed(words, "hellobtc")
>>> seed
"\xb8\x94\xc79\xc6v\x07VY:\xfd\xb9J\x1d)\xffu3\x0c\x1d'\xd1F\xed\xe5c{R\xb9M\xdbu+\xdc\xc3\xb7\xc34\xe0\x81\xca\x97\x98W\xcf\xab\xa6\xa4c\xf3\xc9\x1d\xc0\xee\xd2\xa2{\xdaX+\x82\x14R\xfa"
>>> base58.b58encode(seed)
'4h3QDYvyXEZRFeoCztcMybKH4aXkysTEmNqyDG2ZUyLTGvGwWUxXcEefCEB5JYjE8zuh2MSmLKsz9e8SQDpmzhuB'
>>> base58.b58encode_check(seed)
'R9cTcYjTpLGZEKquHyv5MzyfQAEYyRzAFTd9dxqNhKqKCCKsxmwcy27qetTbK8zEZDzLSLf7AjF9L9cuWY6bZ4UGzZ3GQ'
>>>

从种子开始生成 HD 钱包

下面就将上面生成的种子作为 HD 钱包的根种子（root seed），任何 HD 钱包的根种子都可以重新创造整个 HD 钱包。

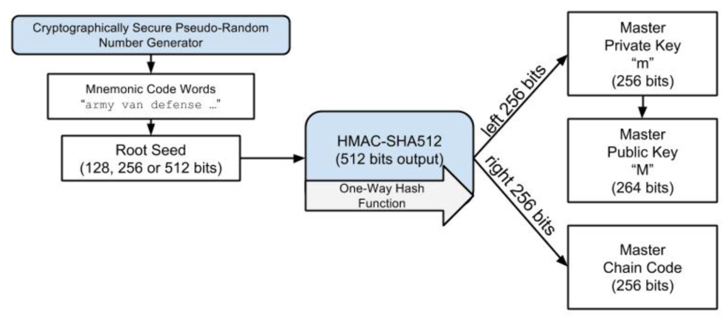
将 root seed 输入到 HMAC-SHA512 算法中可以得到一个 512 位的 Hash，该 Hash 的左边 256 位作为 主私钥 m（Master Private Key），右边 256 位作为 主链码（Master Chain Code）。之后的 主公钥 M（Master Public Key，264 bits）可以通过 主私钥 m 生成。

子密钥衍生函数(Child Key Derivation, CKD)

如上所述，给定 Parent extended key 以及一个索引号(index)，就可以生成相应的 child extended key。

各个子层级的密钥生成规则如下图：

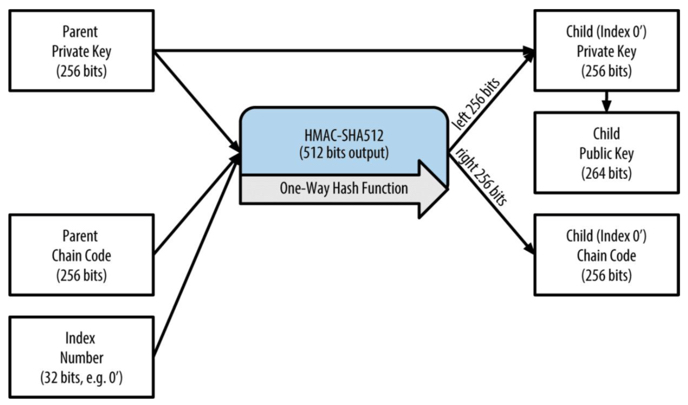
从上图可以看到，HD 的密钥生成如下几个参数：

  • Parent Private Key 或 Parent Public Key；（均为未压缩的 256 bits 的 ECDSA 密钥）；
  • 256 bits 的 Parent Chain Code；
  • 32-bit 整型的 index number（索引号）；

另外，上面的过程是可以递归下去的，图中的 Child Private Key 可以作为其下一层级的 Parent Private Key。

通过将 (Parent Publick Key, Parent Chain Code, Index Number) 输入至 HMAC-SHA512 算法中，我们就可以生成其子密钥，并且我们可以通过调整 Index Number 来生成同一层级的多个子密钥。

关于扩展密钥(extended key)

因为这个密钥衍生函数是单向的，所有 子密钥 都是不能够被用来推导出它们的 父密钥 的，也不能推导出同层级的 姊妹密钥 的，只有 父密钥 和 父链码（又是由 Parent 的 Parent 层级的 密钥 和 链码 生成） 可以推导出所有的 子密钥 和 子链码，后续也就可以生成相应的 子公钥 以及地址，并且用于对交易进行签名。

将 密钥 Key 和 Chain Code 结合起来称为 扩展密钥（extended key），可以通过 扩展密钥 来生成自其而下的所有分支。

扩展密钥 中提供的密钥可以为 私钥 或者 公钥，和 链码 结合起来分别称为 扩展私钥（extended private key） 和 扩展公钥（extended public key），并且分别记为 (k, c) 和 (K, c)，其中公钥 K = point(k)。

我们可以从 扩展私钥 推导出 扩展公钥，而反之则不可以，因此对于某些交易场景（如电商），可以为每笔交易生成一个新的公钥和地址来收款，而扩展私钥可以被存储在纸质钱包或者硬件钱包中，用于安全的离线签署交易。可以看到 扩展公钥 的安全性相对高一些，下图为通过 扩展 父公钥 来衍生 子私钥进而生成子公钥 的传递机制：

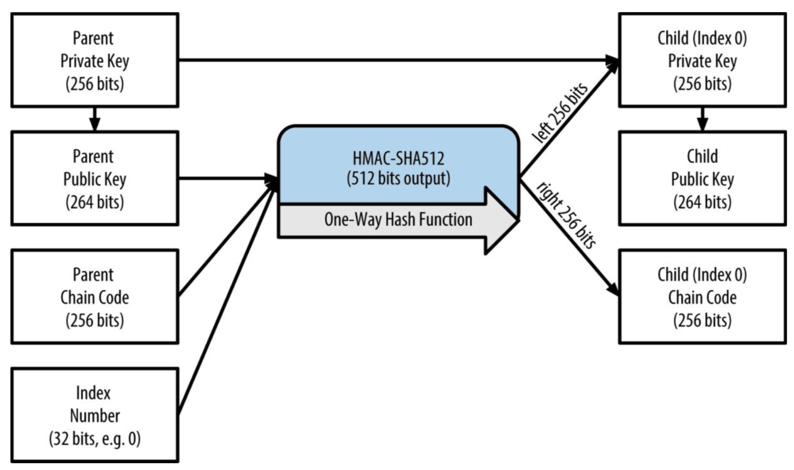
扩展密钥 也通过 Base58Check 进行编码，扩展私钥 和 扩展公钥 的编码分别以 xprv 和 xpub 作为前缀。

硬化衍生子密钥 又是什么鬼？

上面的 扩展密钥（尤其是 扩展公钥） 生成的钱包应该够安全的了，但是设计这一套钱包密钥生成算法的工程师觉得还不够：即使暴露了 扩展公钥，也就是暴露了 子公钥 和 Chain Code，但是如果哪天不小心，你那个 子私钥 也不小心泄露了，那么以这个 子密钥和 Chain Code 作为根的那棵树上挂着的所有的密钥也都能够被推导出来了，这TM太危险了（是的，你要是把你的 root seed 泄露了，估计够你哭三天三夜的~没币除外）。

然后 HD 钱包又提出来一种叫做 硬化衍生(hardened derivation) 的衍生函数，从上面 扩展公钥 生成的图中可以看到 子密钥 和 子链码 都是由 父公钥 和 父链码 通过 HMAC-SHA512 生成的（也都是相对比较容易“曝光”的），而 硬化衍生 函数将 父公钥 换成 父私钥 来推导出 子密钥 和 子链码，如下图：

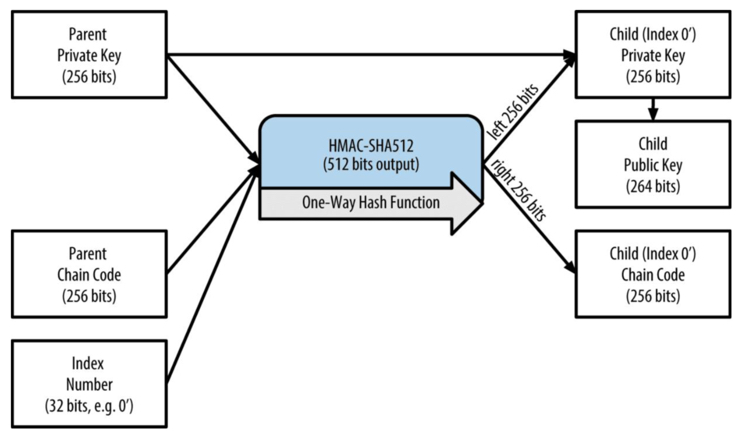
  • 图上标识了 索引号码 根据 正常衍生 和 硬化衍生 不同，索引的范围不同，对于正常衍生的索引号范围为 [0x0, 0x7FFFFFFF]，而硬化衍生的索引号范围为 [0x80000000, 0xFFFFFFFF]；
  • 硬化衍生的索引号太长，一般为了便于阅读，都是会将索引号右上角加上撇号，譬如：0x80000000 记为 0’，0x80000001 记为 1’，以此类推；

总结

针对 扩展密钥 的学习，可以看到有三种生成规则，分别如下：

  1. Private parent key -> private child key

即，从 父扩展私钥 和 父链码 计算生成 子扩展私钥 和 子链码。用公式表示就是：

1
CKDpriv((kpar, cpar), i) → (ki, ci)
  1. Public parent key -> public child key

即，从 父扩展公钥 和 父链码 计算生成 子扩展公钥 和 子链码。公式表示如下：

1
CKDpub((Kpar, cpar), i) → (Ki, ci)
  1. Private parent key -> public child key

即，从 父扩展私钥 和 父链码 计算生成 子扩展公钥 和 子链码。公式表示如下：

1
N((k, c)) → (K, c)

下面是根据自己理解整理的 HD Wallet 的分层密钥生成结构图如下：

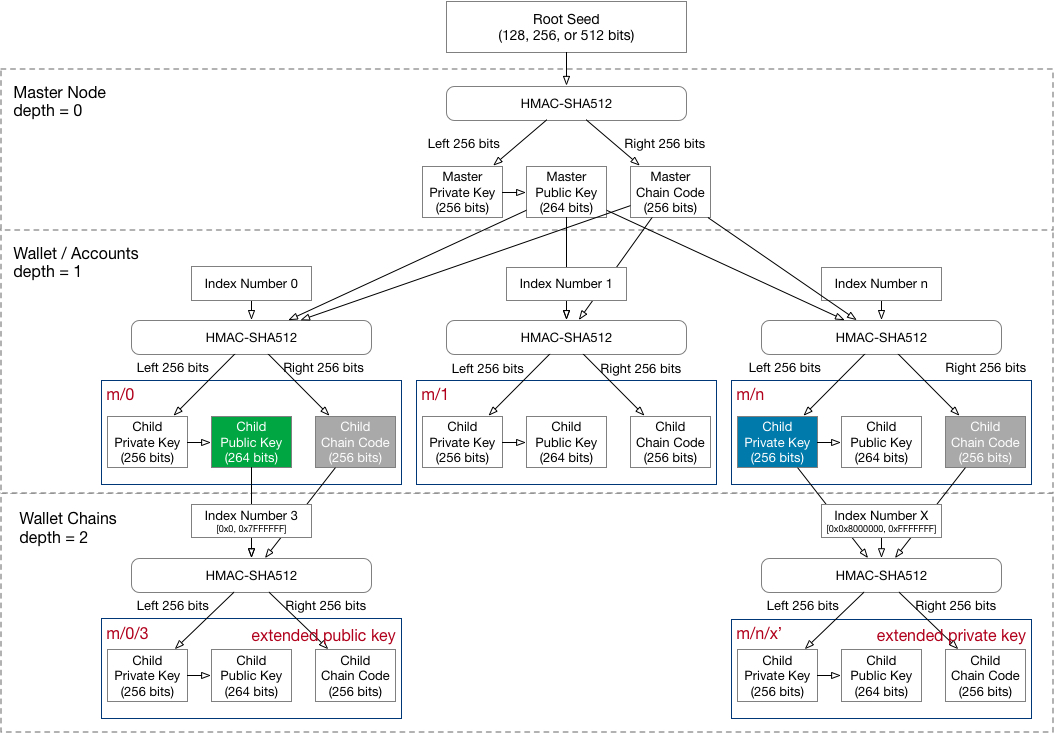
参考来源

Welcome to my other publishing channels